DATA101
[알고리즘] 선택 정렬에 대해 알아보자! (+Python 구현) 본문
본 포스팅에서는 선택 정렬(selection sort) 알고리즘에 대해 알아봅니다.
📚 목차
1. 선택 정렬이란?
2. 선택 정렬의 동작 과정
3. 선택 정렬 구현(Python)
4. 선택 정렬의 시간 복잡도
1. 선택 정렬이란?
선택 정렬은 여러 개의 데이터가 무작위로 있을 때 전체 데이터에서 매번 가장 작은(또는 가장 큰) 데이터를 선택하여 데이터 간의 위치를 변경하는 과정을 반복하여 데이터를 오름차순(또는 내림차순)으로 정렬할 때 사용합니다. 선택 정렬의 종류는 2가지로 나눌 수 있습니다.
- 최소 선택 정렬(Min-selection sort): 매번 가장 작은 데이터를 선택하고 데이터 간의 배치를 변경하며 오름차순으로 정렬
- 최대 선택 정렬(Max-selection sort): 매번 가장 큰 데이터를 선택하고 데이터 간의 배치를 변경하며 내림차순으로 정렬
2. 선택 정렬의 동작 과정
최소 선택 정렬의 경우 구체적인 동작 과정은 다음과 같습니다.
1️⃣ 전체 데이터에서 가장 작은 데이터를 선택하고 맨 앞에 있는 데이터와 자리를 바꿉니다.
2️⃣ 그다음으로 작은 데이터를 선택하고 맨 앞에서 두 번째 데이터와 자리를 바꿉니다.
3️⃣ 위와 같은 방식으로 오름차순으로 정렬이 완료될 때까지 데이터를 선택하고 자리를 바꾸는 과정을 반복합니다.
이제 예시와 함께 선택 정렬의 구체적인 동작 과정을 알아보도록 하겠습니다. 그림 1 과 같이 정렬 없이 정수 10개가 무작위로 배치되어 있을 때 선택 정렬을 활용해서 오름차순으로 정렬해 보도록 하겠습니다.

편의상 정렬되지 않은 데이터 중에서 가장 작은 값을 파란색으로, 정렬된 데이터는 회색으로 표현하겠습니다. 추가로 가장 작은 값과 자리를 변경할 데이터를 파란색 화살표로 표시하겠습니다.
(1) 정렬되지 않은 데이터에서 가장 작은 값인 0을 선택하고 맨 앞에 있는 값인 8과 자리를 바꿉니다.

(2) 정렬되지 않은(회색 제외) 데이터에서 가장 작은 값인 1을 선택하고 맨 앞에 있는 값인 3과 자리를 바꿉니다.

(3) 정렬되지 않은(회색 제외) 데이터에서 가장 작은 값인 2를 선택하고 맨 앞에 있는 값인 8과 자리를 바꿉니다.
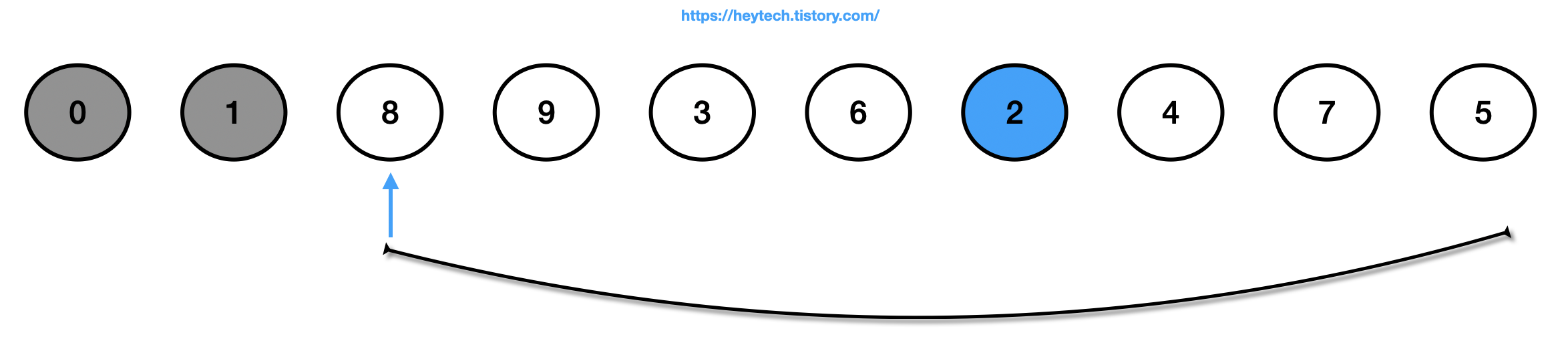
(4) 정렬되지 않은(회색 제외) 데이터에서 가장 작은 값인 3을 선택하고 맨 앞에 있는 값인 9와 자리를 바꿉니다.
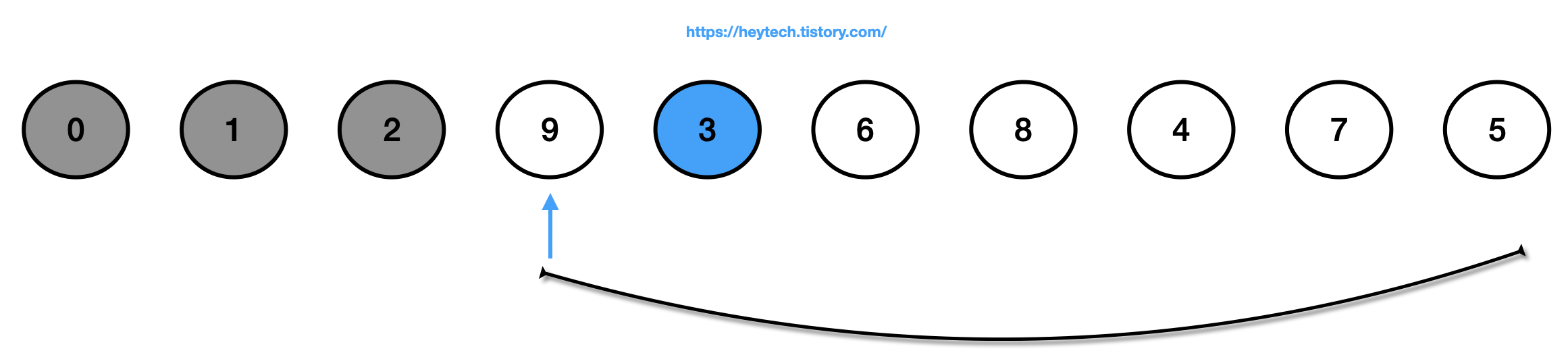
(5) 정렬되지 않은(회색 제외) 데이터에서 가장 작은 값인 4를 선택하고 맨 앞에 있는 값인 9와 자리를 바꿉니다.
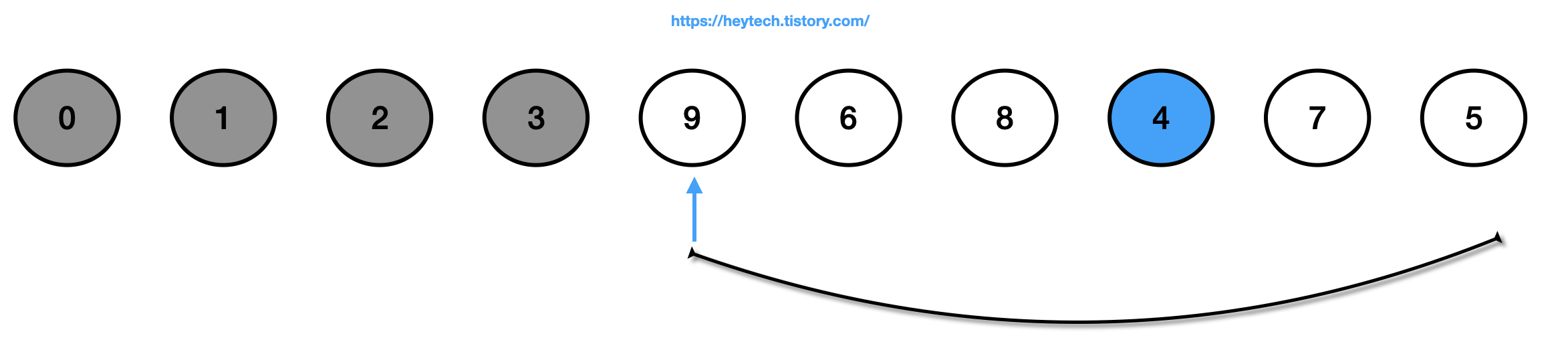
(6) 정렬되지 않은(회색 제외) 데이터에서 가장 작은 값인 5를 선택하고 맨 앞에 있는 값인 6과 자리를 바꿉니다.

(7) 정렬되지 않은(회색 제외) 데이터에서 가장 작은 값인 6을 선택하고 맨 앞에 있는 값인 8과 자리를 바꿉니다.

(8) 정렬되지 않은(회색 제외) 데이터에서 가장 작은 값인 7을 선택하고 맨 앞에 있는 값인 9와 자리를 바꿉니다.

(9) 정렬되지 않은(회색 제외) 데이터에서 가장 작은 값인 8을 선택하고 맨 앞에 있는 값인 9와 자리를 바꿉니다.

마지막 (9) 과정을 거치면 전체 데이터가 오름차순으로 정렬됩니다. 이처럼 데이터 N개가 주어졌을 때 가장 작은 데이터를 N-1번 앞으로 보내는 과정을 통해 정렬을 완료할 수 있습니다.
3. 선택 정렬 구현(Python)
arr = [8, 3, 0, 9, 1, 6, 2, 4, 7, 5]
n = len(arr)
for i in range(n):
# 가장 작은 데이터의 인덱스
min_idx = i
for j in range(i+1, n):
# 최솟값 찾기
if (arr[min_idx] > arr[j]):
min_idx = j
# 데이터 간의 자리 변경
arr[i], arr[min_idx] = arr[min_idx], arr[i]
print(arr)앞서 살펴본 예시를 파이썬을 통해 구현한 소스코드는 위와 같습니다.
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]위와 같이 10개의 정수가 오름차순으로 정렬되어 출력되는 것을 확인하실 수 있습니다.
4. 선택 정렬의 시간 복잡도
선택 정렬의 시간 복잡도를 계산하면 다음과 같습니다. 앞서 살펴본 것처럼 N개의 데이터가 있을 때 N-1번만큼 가장 작은 데이터를 찾고 맨 앞으로 보내는 과정이 필요합니다. 구현 방식에 따라 미세한 차이가 있을 수 있지만, 앞서 예시로 활용한 그림처럼 구현하게 되면 총 연산 횟수는 아래 수식 1 만큼 필요합니다.
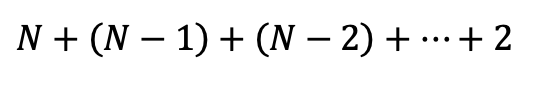
이를 근사치로 계산하면 수식 2 와 다음과 같습니다.
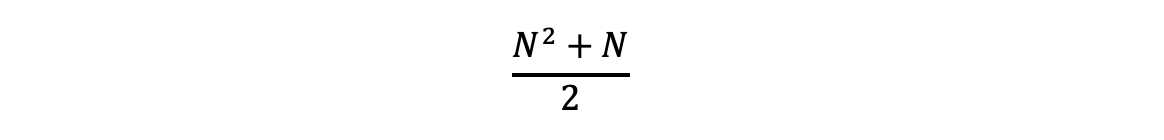
수식 2 는 빅오 표기법으로 간략하게 O(N^2) 으로 표기할 수 있습니다. 이는 위에서 선택 정렬을 구현할 때 이중 반복문을 활용했기 때문에 시간 복잡도가 O(N^2) 라는 것을 직관적으로 이해할 수 있습니다. 이와 같이 선택 정렬은 데이터의 개수가 100배 늘어나면 이론적으로 수행 시간이 10,000배 늘어납니다. 즉, 데이터 개수가 10,000개 이상이면 정렬 속도가 매우 느려질 만큼, 선택 정렬은 시간 복잡도 측면에서 퀵 정렬과 같은 다른 정렬 방법이나 파이썬 내장 라이브러리를 활용한 정렬 방식과 비교했을 때 비효율적입니다.
📚 참고할 만한 포스팅
1. [알고리즘] 선택 정렬에 대해 알아보자! (+Python 구현)
2. [알고리즘] 삽입 정렬에 대해 알아보자! (+Python 구현)
3. [알고리즘] 퀵 정렬에 대해 알아보자! (+Python 구현)
4. [알고리즘] 계수 정렬에 대해 알아보자! (+Python 구현)
5. [파이썬] 내장 함수를 활용한 데이터 정렬하기! (sorted, sort 함수)
포스팅 내용에 오류가 있을 경우 댓글 남겨주시면 감사드리겠습니다.
그럼 오늘도 즐거운 하루 보내시길 바랍니다 :)
고맙습니다.
'알고리즘 > 이론' 카테고리의 다른 글
| [알고리즘] 퀵 정렬에 대해 알아보자! (+Python 구현) (0) | 2021.03.12 |
|---|---|
| [알고리즘] 삽입 정렬에 대해 알아보자! (+Python 구현) (2) | 2021.03.11 |
| [Python] BFS 알고리즘 개념 및 실습 (7) | 2021.03.09 |
| [알고리즘] 깊이 우선 탐색(DFS) 알고리즘에 대해 알아보자!(+Python 구현) (0) | 2021.03.08 |
| 큐(Queue) 자료구조 이해(+ Python) (0) | 2021.03.06 |




