DATA101
[딥러닝] 경사 하강법(Gradient Descent) 종류 본문
📚 목차
1. 경사 하강법 개념
2. 경사 하강법 종류
2.1. 배치 경사 하강법
2.2. 확률적 경사 하강법
2.3. 미니 배치 경사 하강법
1. 경사 하강법 개념
경사 하강법(Gradient Descent)이란 딥러닝 알고리즘 학습 시 사용되는 최적화 방법(Optimizer) 중 하나입니다. 딥러닝 알고리즘 학습 시 목표는 예측값과 정답값 간의 차이인 손실 함수의 크기를 최소화시키는 파라미터를 찾는 것입니다. 학습 데이터 입력을 변경할 수 없기 때문에, 손실 함수 값의 변화에 따라 가중치(weight) 혹은 편향(bias)을 업데이트해야 합니다. 그럼 어떻게 최적의 가중치나 편향을 찾을 수 있을까요? 최적의 가중치를 찾는 과정을 소개합니다. 최적의 편향을 찾는 과정 역시 절차는 동일합니다. 아래의 그림 1을 예시로 활용하겠습니다. 가로축은 가중치를, 세로축은 손실 함수를 의미합니다. 먼저 임의의 가중치를 선정합니다. 운이 좋다면 손실 함수의 최솟값에 해당되는 가중치를 단번에 선택할 수도 있겠지만 그렇지 않을 확률이 훨씬 높습니다.
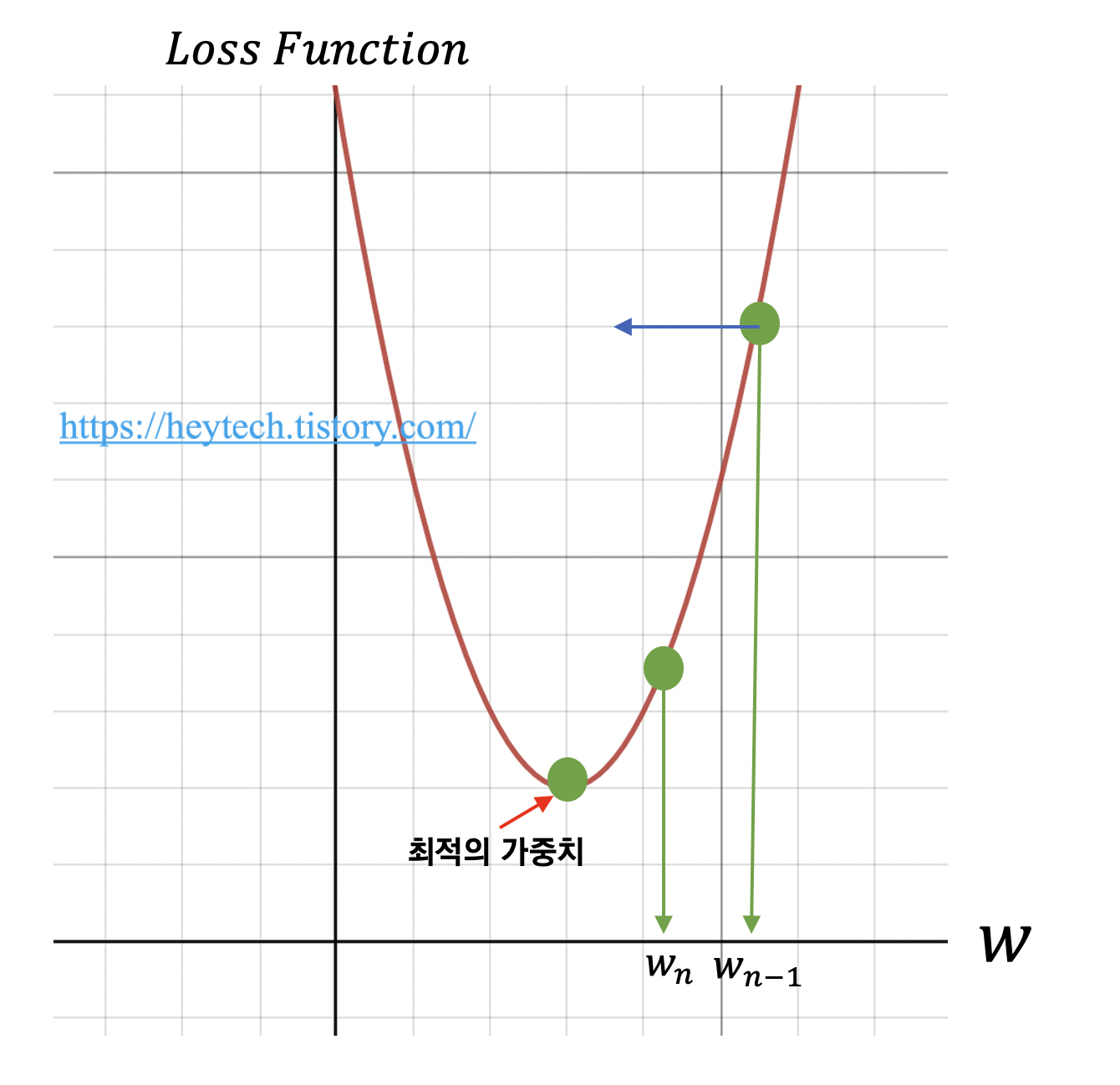
예를 들어, \(w_{n-1}\)을 임의의 가중치로 선정했다고 가정하겠습니다. 최적의 가중치를 찾기 위해서 목표 함수인 손실 함수를 비용 함수 \(w\)에 대해 편미분 하고, 이를 학습률(Learning rate)과 곱한 값을 앞서 선정한 \(w_{n-1}\)에서 빼줍니다. 수식으로 나타내면 다음과 같습니다.
$$ w_{n} = w_{n-1} - \alpha \nabla f(w_{n-1}) $$
위 수식을 통해 손실 함수의 값이 거의 변하지 않을 때까지(약 \(10^{-6}\)) 가중치를 업데이트하는 과정을 반복합니다. 이처럼 손실 함수 그래프에서 값이 가장 낮은 지점으로(=손실 함수의 최솟값) 경사를 타고 하강하는 기법을 경사 하강법이라고 부릅니다.
2. 경사 하강법 종류
본 섹션에서는 경사 하강법의 종류 \(3\)가지를 각각 알아봅니다.
2.1. 배치 경사 하강법
배치 경사 하강법(Batch Gradient Descent)은 가장 기본적인 경사 하강법으로 Vanilla Gradient Descent라고 부르기도 합니다. 배치 경사 하강법은 데이터셋 전체를 고려하여 손실함수를 계산합니다. 배치 경사 하강법은 한 번의 Epoch에 모든 파라미터 업데이트를 단 한 번만 수행합니다. 즉, Batch의 개수와 Iteration은 \(1\)이고 Batch size는 전체 데이터의 개수입니다. 파라미터 업데이트할 때 한 번에 전체 데이터셋을 고려하기 때문에 모델 학습 시 많은 시간과 메모리가 필요하다는 단점이 있습니다.
2.2. 확률적 경사 하강법
확률적 경사 하강법(Stochastic Gradient Descent)은 배치 경사 하강법이 모델 학습 시 많은 시간과 메모리가 필요하다는 단점을 개선하기 위해 제안된 기법입니다. 확률적 경사 하강법은 Batch size를 \(1\)로 설정하여 파라미터를 업데이트하기 때문에 배치 경사 하강법보다 훨씬 빠르고 적은 메모리로 학습이 진행됩니다.

위의 그림 2는 경사 하강법 종류에 따라 최적의 해를 찾아가는 과정을 시각화한 자료입니다. 좌측은 확률적 경사 하강법을, 우측은 배치 경사 하강법을 활용한 경우입니다. 확률적 경사 하강법은 파라미터 값의 업데이트 폭이 불안정하기 때문에 배치 경사 하강법보다 정확도가 낮은 경우가 생길 수도 있습니다. 그럼에도 불구하고, 하나의 데이터(Batch size=\(1\))에 대해서만 손실함수를 계산하고 파라미터를 업데이트하면 되기 때문에, 적은 시간과 메모리로도 모델을 학습시킬 수 있다는 장점이 있습니다.
2.3. 미니 배치 경사 하강법
미니 배치 경사 하강법(Mini-Batch Gradient Descent)은 Batch size가 \(1\)도 전체 데이터 개수도 아닌 경우를 말합니다. 미니 배치 경사 하강법은 배치 경사 하강법보다 모델 학습 속도가 빠르고, 확률적 경사 하강법보다 안정적인 장점이 있습니다. 덕분에, 딥러닝 분야에서 가장 많이 활용하는 경사 하강법입니다. 그럼 Batch size는 어떻게 정하면 좋을까요? 일반적으로 \(32\), \(64\), \(128\)과 같이 \(2\)의 \(n\) 제곱에 해당하는 값으로 사용하는 게 보편적입니다.
포스팅 내용에 오류가 있다면 아래에 댓글 남겨주시길 바랍니다.
그럼 오늘도 즐겁고 건강한 하루 보내시길 바랍니다 :)
고맙습니다😊
'AI & 빅데이터 > 머신러닝·딥러닝' 카테고리의 다른 글
| [딥러닝] Grid Search, Random Search, Bayesian Optimization (0) | 2022.05.23 |
|---|---|
| [딥러닝] 기울기 소실(Vanishing Gradient)의 의미와 해결방법 (12) | 2022.05.22 |
| [딥러닝] Epoch, Iteration, Batch size 개념 (6) | 2022.05.21 |
| [Deep Learning] 최적화(Optimizer): (4) Adam (0) | 2022.05.21 |
| [Deep Learning] 최적화(Optimizer): (3) RMSProp (0) | 2022.05.21 |




