DATA101
[딥러닝] 기울기 소실(Vanishing Gradient)의 의미와 해결방법 본문
📌 Text 빅데이터분석 플랫폼 베타테스트 참가자 모집 중!(네이버페이 4만 원 전원 지급)

👋 안녕하세요, 코딩이 필요 없는 AI/빅데이터 분석 All in One 플랫폼 <DATA101> 개발팀입니다.
😊 저희 서비스를 사용해 보시고 경험담을 들려주세요 :)
💸 참여해 주신 "모든" 분들께 네이버페이 4만 원 쿠폰을 지급해 드립니다.
👨💻 참여 희망 시 카톡플러스친구 1:1 채팅 or 인스타그램 DM 부탁드립니다 :)
📆 참여기간 : 11/25(월)~11/29(금) 11:00~21:00 중 택1 (1시간 1타임)
👉 참여장소 : 강남역 인근 스터디카페 미팅Room
📍 소요시간 : 총 40분 내외(서비스 체험 및 인터뷰 포함)
✅ 참가조건 : Text 빅데이터 분석 업무 경험자
👉 참가 가능일정 조회하기 : https://url.kr/n8k8gu
- 카톡플친 : http://pf.kakao.com/_SxltHG/chat
- 인스타그램 : https://www.instagram.com/data101.official/
📚 목차
1. 기울기 소실의 의미
2. 기울기 소실의 원인
3. 기울기 소실의 해결방법
1. 기울기 소실의 의미
딥러닝 분야에서 Layer를 많이 쌓을수록 데이터 표현력이 증가하기 때문에 학습이 잘 될 것 같지만, 실제로는 Layer가 많아질수록 학습이 잘 되지 않습니다. 바로 기울기 소실(Vanishing Gradient) 현상때문입니다. 기울기 소실이란 역전파(Backpropagation) 과정에서 출력층에서 멀어질수록 Gradient 값이 매우 작아지는 현상을 말합니다(그림 1 참고). 그렇다면 왜 이런 기울기 소실 문제가 발생할까요? 이어지는 섹션에서 자세히 알아봅니다.

2. 기울기 소실의 원인
기울기 소실의 발생 원인은 활성화 함수(Activation Function)의 기울기와 관련이 깊습니다.
2.1. Sigmoid 함수
활성화 함수 중 Sigmoid 함수를 예로 들어보겠습니다(그림 2 참고). 그림 2의 우측 그래프에서 볼 수 있듯이, Sigmoid 함수의 미분 값은 입력값이 \(0\)일 때 가장 크지만 \(0.25\)에 불과하고 \(x\) 값이 크거나 작아짐에 따라 기울기는 거의 \(0\)에 수렴하는 것을 확인하실 수 있습니다. 따라서, 역전파 과정에서 Sigmoid 함수의 미분값이 거듭 곱해지면 출력층과 멀어질수록 Gradient 값이 매우 작아질 수밖에 없습니다. 더불어, \(e\)(exponential)는 컴퓨터가 계산할 때 정확한 값이 아닌 근사값으로 계산해야 되기 때문에 역전파 과정에서 점차 학습 오차까지 증가하게 됩니다. 결국 Sigmoid 함수를 활용하면 모델 학습이 제대로 이루어지지 않게 됩니다.
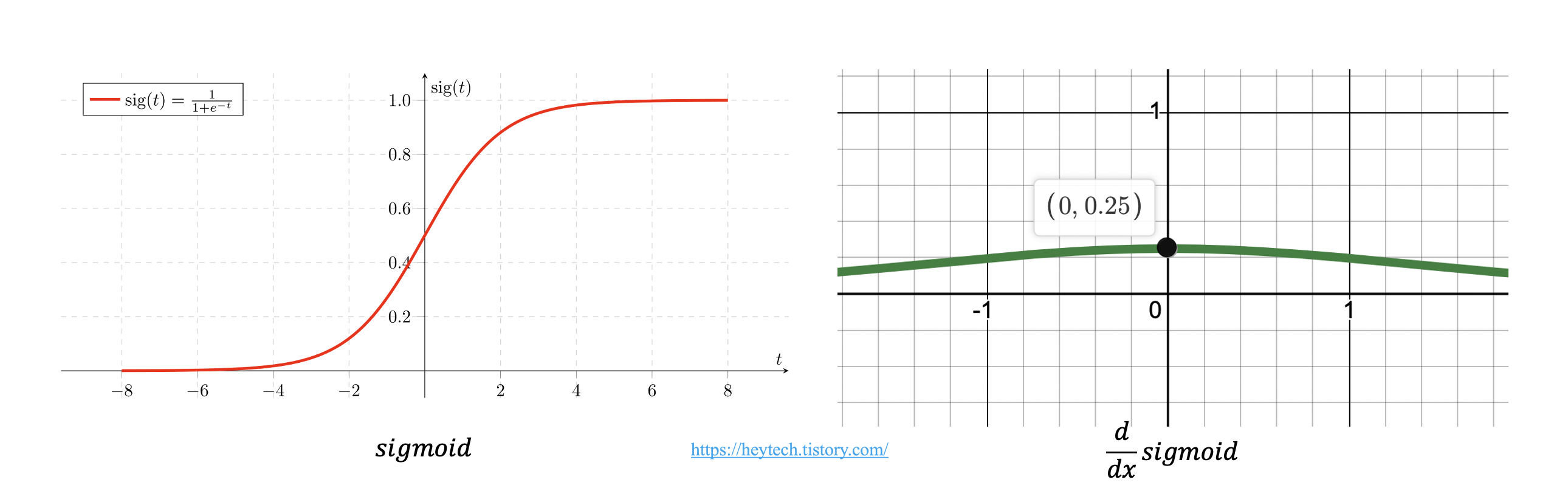
2.2. tanh 함수
역전파 과정에서 Sigmoid 함수가 층이 많아질수록 효과적으로 학습되지 않는 한계점을 개선하기 위한 방법 중 하나로 tanh 함수가 제안되었습니다. Simoid 함수와 다르게, tanh 함수는 \(0\)을 기준으로 출력 값이 최대 \(1\), 최소 \(-1\) 사이의 값을 갖도록 출력값의 범위를 2배 늘렸습니다. 그림 3 내 우측 그래프에서 볼 수 있듯이, 이를 통해 미분값이 sigmoid 함수에 비해 훨씬 커졌습니다. 하지만, 그럼에도 tanh 함수 역시 \(x\) 값이 크거나 작아짐에 따라 기울기 크기가 크게 작아지게 떄문에 기울기 소실 문제를 방지하는 데 어려움이 있습니다. 기울기 소실 문제를 해결한 활성화 함수로 ReLU가 제안되었습니다. 다음 섹션에서 ReLU에 대해 자세히 다룹니다.
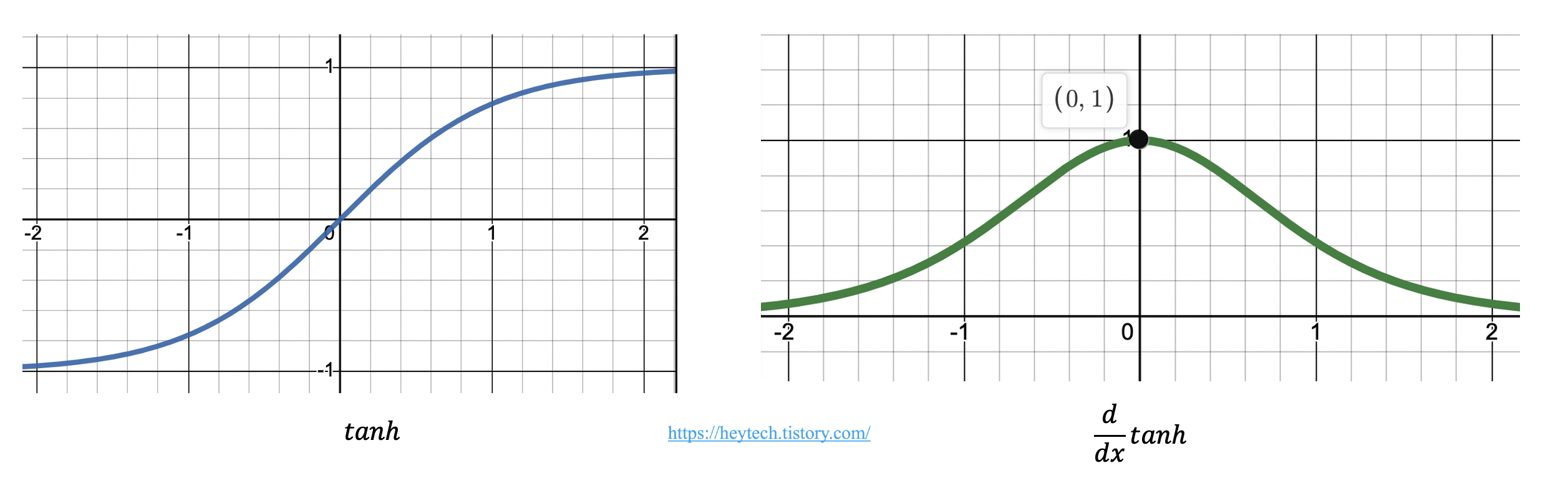
3. 기울기 소실의 해결방법
Simoid, tanh 함수 모두 기울기 소실 문제가 있었습니다. ReLU 함수는 이러한 문제를 해결하기 위해 제안되었습니다. 본 섹션에서는 기본적인 ReLU 함수와 변형된 ReLU 함수에 대해 알아봅니다.
3.1. ReLU 함수
아래의 그림 4에 우측 그래프에서 보실 수 있듯이, 입력값이 양수일 경우, 입력값에 상관 없이 항상 동일한 미분 값은 \(1\)입니다. 즉, 역전파 과정에서 기울기가 소실되는 문제를 해결할 수 있습니다. 더불어, ReLU 함수는 Simoid, tanh 함수처럼 특별한 연산이 필요 없이 단순히 임계값(\(0\))에 따라 출력값이 결정되므로 연산 속도 또한 빠르다는 특징이 있습니다.
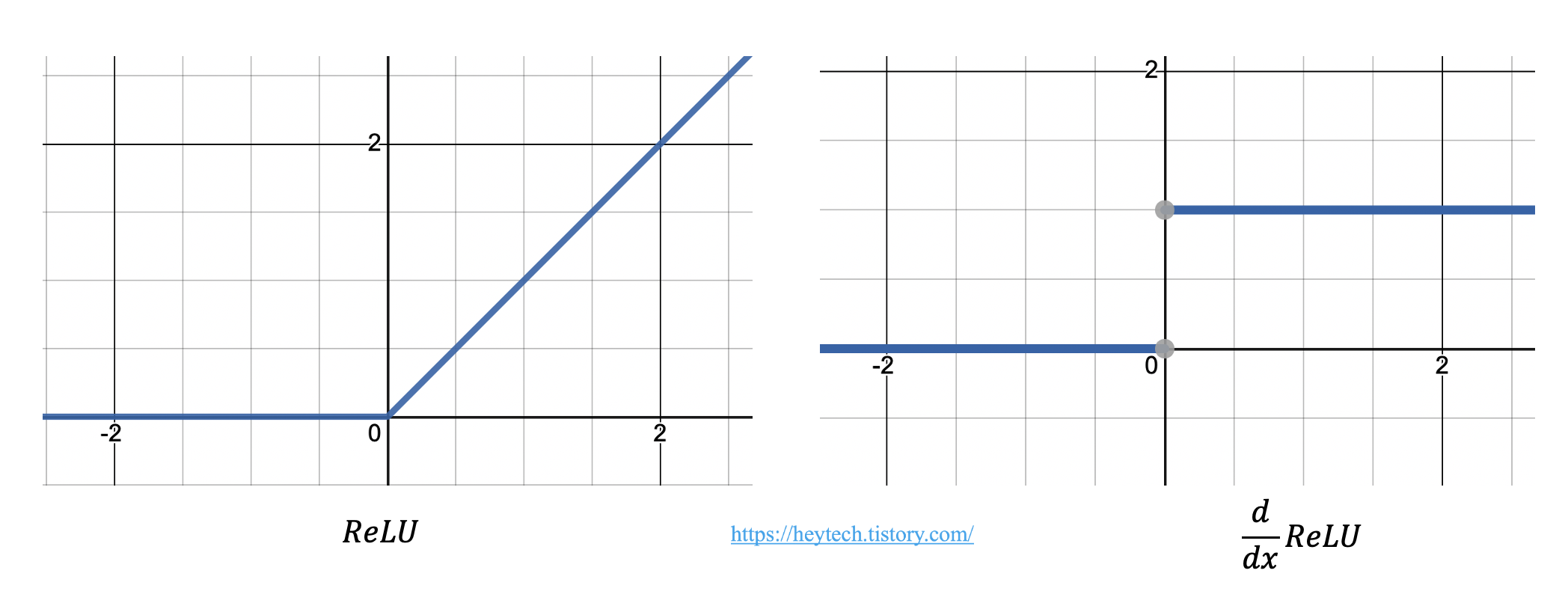
하지만 ReLU 함수 역시 한계점이 존재합니다. 입력값이 음수일 경우 미분값은 항상 \(0\)입니다. 즉, 입력값이 음수인 뉴런은 다시 회생시키기 어렵다는 한계가 있습니다. 이러한 문제를 '죽어가는 ReLU(Dying ReLU)'라고 부릅니다.
3.2. Leaky ReLU 함수
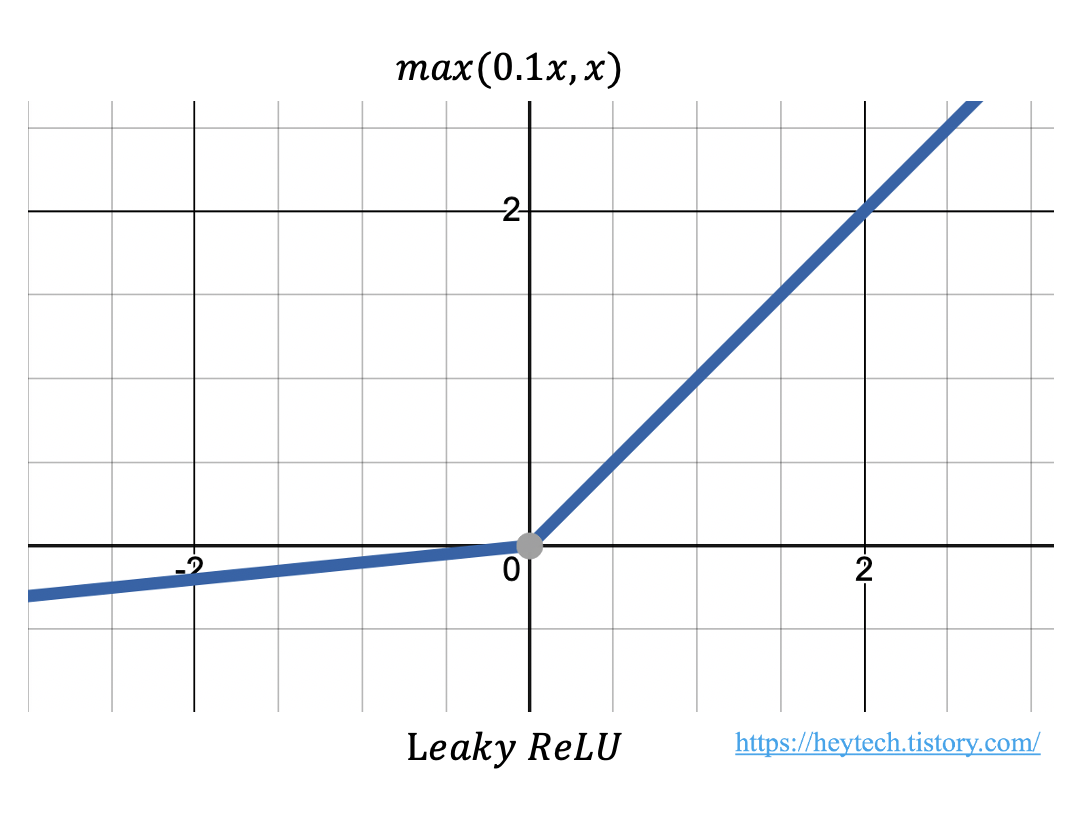
ReLU 함수에서 발생하는 Dying ReLU 현상을 보완하기 위해 다양한 변형된 ReLU 함수가 제안되었습니다. 그중에서 Leaky ReLU에 대해 알아봅니다. Leaky ReLU는 입력값이 음수일 때 출력값을 \(0\)이 아닌 \(0.001\)과 같은 매우 작은 값을 출력하도록 설정합니다. 수식은 다음과 같습니다.
$$ max(ax, x) $$
여기서 \(a\)는 \(0.01, 0.001\)과 같이 작은 값 중 하나로 하이퍼파라미터입니다(그림 5 참고). Leaky는 사전적으로 '(물이나 연기 등이)새어 나가는' 같은 의미가 있습니다. 여기서 말하는 '새어 나가는' 정도는 입력값이 음수인 경우의 기울기를 나타냅니다. 이처럼 \(a\)는 \(0\)이 아닌 값이기 때문에 입력값이 음수라도 기울기가 \(0\)이 되지 않아 뉴런이 죽는 현상을 방지할 수 있습니다.
포스팅 내용에 오류가 있거나 보완할 점이 있다면 아래에 👇👇👇 댓글 남겨주시면 감사드리겠습니다 :)
그럼 오늘도 즐겁고 건강한 하루 보내시길 바랍니다.
고맙습니다😊
'AI & 빅데이터 > 머신러닝·딥러닝' 카테고리의 다른 글
| 딥러닝 모델 평가 지표: Confusion Matrix, Accuracy, Precision, Recall, F1 Score, Average Precision (0) | 2022.07.14 |
|---|---|
| [딥러닝] Grid Search, Random Search, Bayesian Optimization (0) | 2022.05.23 |
| [딥러닝] 경사 하강법(Gradient Descent) 종류 (0) | 2022.05.21 |
| [딥러닝] Epoch, Iteration, Batch size 개념 (6) | 2022.05.21 |
| [Deep Learning] 최적화(Optimizer): (4) Adam (0) | 2022.05.21 |




